(III)В истории экономической мысли исчезли работы В.Дмитриева, хотя они являются теоретической базой всей современной экономики, в частности, системы национальных счетов, межотраслевых балансов и т.д. Они требуют рассматривать экономику как целостную систему.
В 1900 г. в типографии Московского университета был напечатан первый научный труд Владимира Карповича «Экономические очерки. Выпуск первый. Теория ценности Д. Рикардо (Опыт точного анализа)». Этой работой он заявил о себе как о первом российском экономисте-математике. В 1902 г. он публикует продолжение своего научного труда «Экономические очерки»: «Очерк II. Теория конкуренции Or. Курно» и «Очерк III. Теория предельной полезности».
В 1904 г. все три ранее опубликованных экономических очерка были изданы отдельной книгой «Экономические очерки. (Серия 1-я: Опыт органического синтеза теории ценности и теории предельной полезности)». В.Дмитриев предполагал подготовить еще одну серию из трех очерков: по теории ренты, промышленных кризисов и денежного обращения. По всей видимости, эти труды написаны не были.
Владимир Карпович Дмитриев родился 24 ноября 1868 г. в имении «Рай» Смоленской губернии и уезда. Образование он получил сначала в Тульской классической гимназии, где учился с П.Струве. Гимназию он окончил в 1888 г. Затем поступил в Московский университет сначала на медицинский факультет, а потом перешел на юридический; на последнем курсе он начинает уже свое исследование о ценности. Окончив в 1896 г. университет, он женился на Т.А. Ватаци и уехал на первое попавшееся ему место акцизного контролера в местечке Воньковцы в Подольской губернии. На службе он пробыл три года, открывшийся туберкулез заставил его бросить службу и эта тяжелая болезнь не оставляла его до самой смерти. Она же и свела его 30 сентября 1913 г. в могилу. В.К.Дмитриев всю жизнь очень нуждался; плохие материальные условия и недостаток средств для лечения, бесспорно, ускорили его кончину.
По мнению авторов, настойчивое замалчивание В.Дмитриева в СССР и России связано с тем, что он подверг критике марксизм. Но не меньше критики от него досталось политизированной и далекой от экономики либеральной школе. Он утверждал в своих работах, что объективные экономические законы ничего общего не имеют с политикой. В.Дмитриев отстаивал всем хорошо известный тезис – объективные законы и реальность даны нам в ощущения, но независимы от нашего сознания. Из этого следует, что если законодатели, политики той или иной страны не знают этих законов, то законодательство в этих странах отличается повышенной коррупционной емкостью, а декларируемая борьба с коррупцией является политическим кокетством или благими пожеланиями, с помощью которых умащивается дорога в ад. Поэтому общество будет жить в бесконечных кризисах. А либеральные экономисты будут настойчиво «доказывать» обществу, что «кризисы перепроизводства» неизбежны. А также, что кризисы служат для «очищения» экономики. Если они имели в виду процесс очищения карманов у 95 % населения, то это правда.
В.Дмитриев первым отделил экономику, ее объективные законы от политики и от политических заказов экономистам на проведение «научных исследований», оправдывающих бездарное управление «элиты» общества и получающих за это Нобелевские премии.
Свои экономические очерки В.Дмитриев начинает с замечательных цитат, актуальность которых и в двадцать первом веке не утрачена.
Никакое человеческое исследование не может назваться настоящим знанием, если не прошло через математические доказательства
Я утверждаю, что во всяком естественно-научном знании можно найти лишь столько действительной науки, сколько в нем можно найти математики
Применение математики должно же иметь место там, где невозможно достигнуть истины без ее содействия. Если бы в других отраслях знаний существовало такое же отвращение к математическому анализу, как в политической экономии, то мы остались бы в совершенном неведении относительно важнейших законов природы.
Простейшей формулой зависимости цены от издержек производства является формула
1 Например, Буагильберу (Bois-Guillebert P. Les details de la France. Paris, 1843). Ср.: Marx K. Zur Kritik der politischen Okonomie. Berlin, 1859. S. 32; Зибер Н.И. Давид Рикардо и Карл Маркс в их экономических исследованиях. М., 1885.
Чтобы перейти от этого факта к законченной теории издержек производства, экономической науке предстояло,
во-первых, указать законы, определяющие величину того излишка, который возмещается в цене сверх сделанных затрат;
во-вторых, анализировать самые затраты, делаемые предпринимателем при производстве продукта.
Первая задача не была удовлетворительно разрешена даже и Смитом: величина прибыли, как известно, определяется у него отношением спроса и предложения капиталов, т.е. моментом, зависящим от условий рынка.
Что касается анализа реальных издержек производства (т.е. издержек производства в тесном смысле слова, не включая сюда прибыли,) то и здесь до Смита было сделано весьма немного.
1 Например, Буагильберу (Bois-Guillebert P. Les details de la France. Paris, 1843). Ср.: Marx K. Zur Kritik der politischen Okonomie. Berlin, 1859. S. 32; Зибер Н.И. Давид Рикардо и Карл Маркс в их экономических исследованиях. М., 1885.
Самый подробный анализ издержек производства находим мы в трудах ближайшего предшественника Смита — Стеварта.
«Действительная ценность вещи, по учению Стеварта (Stewart J.), слагается из следующих элементов: из «ценности средств существования рабочего и необходимых расходов, как для удовлетворения его личных потребностей, так и для обеспечения инструментами, необходимыми в его профессии» и из «ценности материалов, то есть первого предмета используемого рабочим».
Совокупностью этих трех элементов определяется, по Стеварту, низший предел, дальше которого не может упасть рыночная цена продукта. Мы видим здесь, в сущности, простой подробный перечень тех затрат, которые делает капиталист-производитель (прибыль по-прежнему ставится в зависимость от условий рынка, т.е. от спроса и предложения данного товара); никаких следов научного анализа в этом «учении» об издержках производства еще не замечается.
Единственным исключением является учение о материальной заработной плате: уже до появления труда А. Смита в экономической науке установилось учение о тенденции материальной заработной платы к необходимым средствам существования.
W. Petty (Political Anatomy of Ireland. L., 1691. P. 64) говорит: «Стоимость средней дневной рабочей платы определяется тем, что нужно рабочему, чтобы жить, работать и размножаться».
A. Turgot (Reflexions sur la formation et la distribution des richesses. 1770. § 6) говорит: «Рабочие принуждены понизить цену наперерыв один другому. Во всех видах труда должно дойти и действительно доходит до того, что плата рабочего ограничивается необходимыми средствами существования».
Впрочем, самый механизм процесса, постоянно удерживающего заработную плату на уровне средств к существованию, был выяснен лишь в труде А. Смита.
Выделенные величины в скобках являются неизвестными.
Понятно, что на этой стадии развития теория издержек производства вполне заслуживает упрека, так часто делаемого теории издержек производства вообще (следовательно, и во вполне развитом ее виде), что
Зибер приводит слова Каморжинского: «Против теорий издержек производства можно возразить то, что цену блага они объясняют не из таких элементов, которые бы были независимы от цены, а из других цен, потому что издержки производства вычисляются из цен всех благ, потребных для производства».
Зибер прибавляет к этому: «Приведенная нами формулировка вопроса, что такое издержки производства, представляет собой яркое выражение того недовольства, которое возникает в умах некоторых — к сожалению, весьма немногих новейших экономистов — при обсуждении терминов, лишь по видимости содержащих известный и определенный смысл...».
А. Смиту предстояла нелегкая задача, и неудивительно поэтому, что он разрешил ее далеко не в полном объеме.
Только в трудах его преемника, Рикардо, теория издержек производства получила свое завершение. Но и Смитом сделано весьма много для верного разрешения проблемы. Прежде всего, мы находим у А. Смита точную постановку самого вопроса, подлежащего разрешению (что, несомненно, является важным для правильного его разрешения).
«Задача теории ценности, — говорит Смит, — выяснить законы, которым естественно повинуются люди при мене товаров один на другой».
Этим прежде всего устранился всякий вопрос о внутренней ценности товаров: задачей исследований должна быть лишь относительная ценность товаров, их меновая пропорция (мы употребляем этот термин, следуя Джевонсу, во избежание путаницы, происходящей от употребления слова «ценность» в двух смыслах: меновой и потребительной; употребление термина «меновая пропорция» делает ненужными какие бы то ни было оговорки о различных смыслах слова «ценность», как это делают Смит и Рикардо).
Затем Смит приступает к анализу понятия издержек производства, или, точнее, к анализу тех элементов, из которых они слагаются на деле для капиталиста-предпринимателя. В учении о заработной плате А. Смит лишь развивает и более обосновывает положение, высказанное уже предшествовавшими экономистами, что реальная заработная плата имеет тенденцию совпадать с необходимыми средствами существования рабочего[11] (сам Смит ссылается по этому вопросу на Кантильона (Смит А. Указ. соч. Кн. I. с. 196); окончательное развитие учения о «железном» законе заработной платы получило, как известно, в трудах Д. Рикардо, поэтому и ближайшее рассмотрение этого вопроса мы откладываем до анализа теории ценности Рикардо).
Главные преобразования, внесенные А. Смитом в формулу издержек производства, касаются 2-го и 3-го члена второй части формулы (II). Смит первый указал, что 2-й член — цена потребленных в производстве орудий и материалов, всегда может быть, в свою очередь, разложен на заработную плату, прибыль и ренту (под прибылью и рентой мы везде будем разуметь «сумму прибыли» и «сумму ренты» в деньгах), так что
«Эти три части, — говорит А. Смит, — непосредственно или окончательно составляют всю цену хлеба. По-видимому, можно бы было думать, что к ним можно присоединить еще четвертую часть, необходимую для возвращения капитала фермера и для вознаграждения за его рабочий скот и земледельческие орудия. Но если вникнуть хорошенько в этот предмет, то нетрудно заметить, что цена каждого орудия для земледелия, как, например, лошади, сама состоит из этих же трех частей: из дохода с земли, на которой она взращена, из труда работника, который кормил и присматривал за нею, и из прибыли фермера, который оплатил доход с земли и содержание работника. Поэтому, хотя хлеб должен оплатить также и цену лошади и ее содержание, тем не менее полная цена его всегда может быть разложена, непосредственно или в окончательном результате, на одни и те же составные части — ренту, труд и прибыль».
Это положение распространяется далее Смитом и на все прочие продукты.
Ввиду сбивчивости взглядов Смита на ренту мы будем в дальнейшем рассматривать только последний случай.
Формула (II) примет тогда вид, при условии, что цена продукта, в конечном счете, сводится только к двум элементам (заработной плате и прибыли):
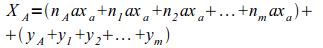(III)
Где
XA — цена продукта A;
nA,n1,n2,…,nm — количество рабочих дней, истраченных в производстве;
Уточнение наше: сюда войдут как рабочие дни, истраченных в производстве собственно продукта А, так и рабочие дни, истраченных на производство орудий и материалов, потребленных при производстве продукта А.
a - количество продукта a, например, хлеба, потребляемого работником в день. Для упрощения формулы мы предполагаем, что рабочий потребляет один продукт, например, хлеб - как некий эталон по оплате труда. Такое же упрощение производит, как известно, в своем анализе и Рикардо. В дальнейшем мы увидим, что принятие нескольких продуктов потребления рабочих ничего не изменяет в нашем анализе;
xa — цена продукта а, например, хлеба;
yA,y1,y2,…,ym— прибыли, вошедшие в состав цены продукта А; сюда войдут как прибыль, полученная собственно производителем продукта А, так и прибыль производителей орудий и материалов, потребленных при производстве продукта А.
Или, если
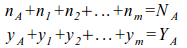
то получим
(IV)
XA=NAaxa + YA
где
XA — цена продукта A;
NA — общая сумма труда, непосредственно или посредственно истраченного в производстве продукта A,
a - количество продукта a, например, хлеба, потребляемого работником в день;
xa — цена продукта а, например, хлеба;
YA — общая сумма прибыли, полученной всеми производителями, непосредственно или посредственно (т.е. производя материалы и орудия) участвовавшими в производстве продукта А.
В сравнительно недавнее время возражения эти опять были выдвинуты (как аргумент против трудовой теории) экономистами «австрийской школы» — сторонниками теории предельной полезности.
Возражения эти сводятся к тому, что в «современном» хозяйстве во всех отраслях производства необходим капитал, потому при вычислении издержек производства нельзя устранить элемент капитала.
Для производства капитала всегда требуется опять капитал. Каким образом, спрашивают они (австрийская школа), можно вычислить количество труда, затраченного для производства данного хозяйственного блага, от самого начала истории, когда человек обходился без капитала, до настоящего времени. Что капитал всегда производится в настоящее время капиталом же, это не подлежит сомнению; справедливо и то, что вычислить количество труда, вошедшего в данный продукт, от момента создания первого капитала одним трудом — дело невозможное.
Обозначим общее количество труда, непосредственно и посредственно затраченного на производство единицы продукта А, через X.
Тогда общая сумма труда, пошедшего на производство единицы продукта А, будет
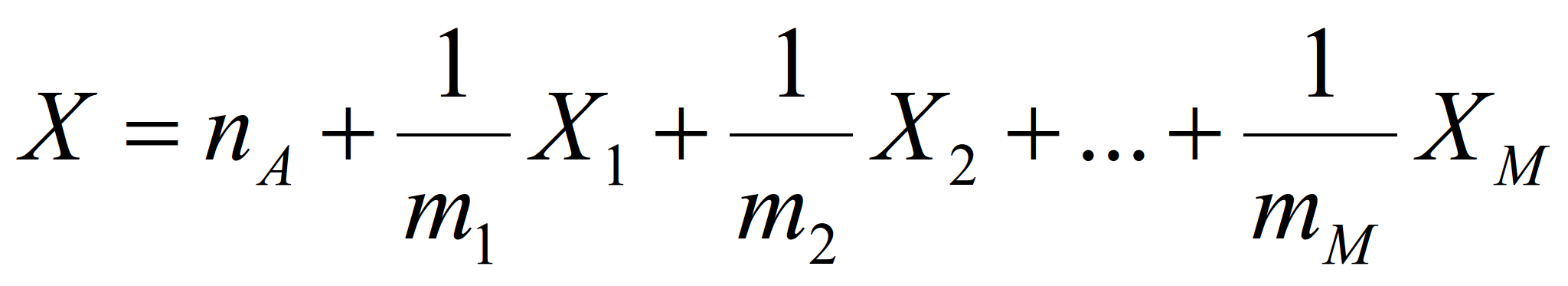(1)
Как nA, так и m1,m2,…,mM здесь величины, данные техническими условиями производства продукта A, неизвестны X1,X2,…,XM.
В производстве капиталов K1,K2,…,KM, которым соответствуют количества труда X1, X2,…,XM этого уравнения, участвуют в свою очередь другие капиталы, как встречающиеся в этом ряду, так и не входящие сюда.
Пусть число всех различных технических капиталов, участвующих как посредственно, так и непосредственно, в производстве продукта А будет U (число всегда конечное).
Уточнение авторов книги. Уже тогда В.Дмитриев настаивает на очевидном факте, что технологии, участвующие как непосредственно, так и посредственно в производстве любого продукта, количество этих технологий КОНЕЧНО. Это очень важный момент, который так и не понял В.Леонтьев, как и другие экономисты, описывающие, использующие МОБ.
В линейной алгебре известно разложение в степенной ряд матриц:
(E-A)-1=1/(E-A)=E+A+A2+…+Am+…
или
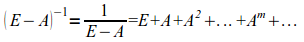
При условии, если Am→0 при m→∞.
Это разложение является принципиальным моментом.
Для математики данный подход достаточно логичен, но в реальной экономике условие Am→0 при m→∞ выглядит как минимум неграмотно.
В производстве любого продукта количество технологий, уровень разделения труда при любой технологической формации естественно конечно, но никогда не может устремляться в бесконечность. Мало того, нам важно разделить индивидуально все и каждую отрасль на конечные уровни технологического разделения труда, а они, как и показывают расчеты:
В этих условиях прямое применение разложения в степенной ряд матриц:
При математическом условии Am→0 при m→∞ экономически бессмысленно и не правильно!!!
Очевидно, что для количества
труда, необходимого для производства
любого капитала Kn из числа
U, можно составить уравнение,
совершенно аналогичное уравнению
Во вторую часть такого уравнения будут входить X, соответствующие капиталам, участвующим в производстве капитала Kn, так как U — число конечное, то получим U уравнений с U неизвестными (X1,X2,X3,…,XU).
Присоединяя сюда уравнение
,
получаем систему из (u+1) уравнений
с (u + 1) неизвестным (X,X1,X2,X3,…,XU),
всегда достаточную для определения X,
которое и дает нам искомую сумму
труда, потраченного на производство
продукта А.
То обстоятельство, что всякий капитал в современных условиях производится сам при содействии другого капитала, как мы видели, нисколько не мешает точному решению вопроса.
Не следует, впрочем, думать, что для определения общей суммы труда, употребленного на производство любого продукта N, непременно понадобится вся система наших (u+1) уравнений; все неизвестные, входящие в выражение этой суммы, могут зачастую исключаться из самого небольшого числа уравнений. Пусть, например, в производстве продукции участвует капитал K1, в производстве капитала K1 – капиталы K2 и K3, в производстве K2 – капиталы K1 и K3, в производстве K3 – капиталы K1 и K2 и т.д.
Тогда, употребляя предыдущие обозначения, будем иметь систему (V) из четырех уравнений с четырьмя неизвестными, из которых X определяется последовательной подстановкой:
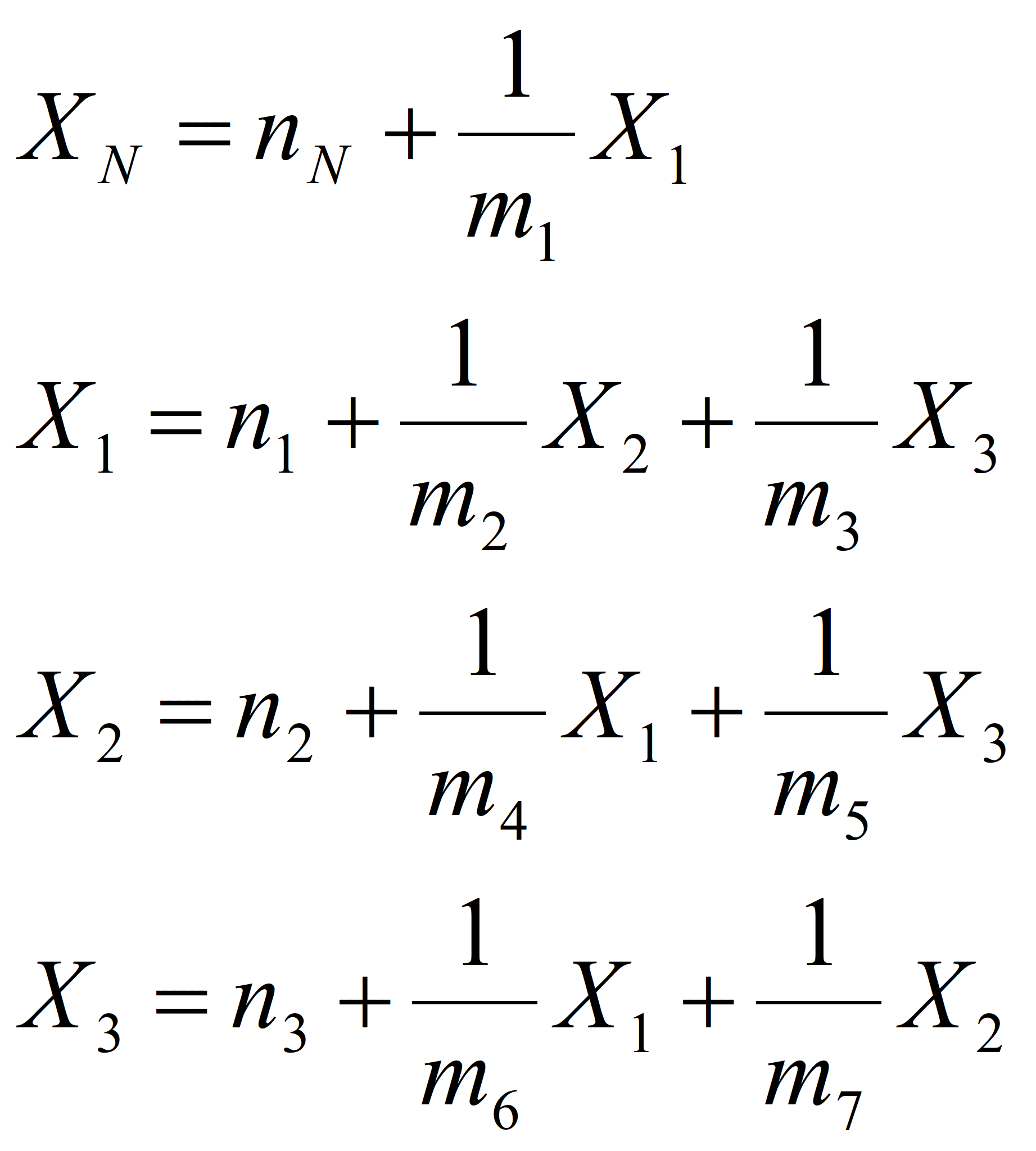(V)
Можно вообразить себе, конечно, и еще более простые случаи.
Примечание: мы никак не можем согласиться с мнением Туган-Барановского (Юридический вестник. 1890. Октябрь. С. 223), который, совершенно справедливо восставая против изложенного возражения на трудовую теорию ценности, делаемого Визером, говорит, что «переходя от одной отрасли промышленности к другой, изготовляющей блага все более и более высших порядков по отношению к нашему продукту... мы дойдем, наконец, до таких отраслей промышленности, которые изготовляют свой собственный постоянный (по терминологии Маркса) капитал». Такое совершенно произвольное предположение лишает решение вопроса необходимой общности.
Не можем мы также признать правильным ни со стороны формы, ни со стороны содержания то «математическое» решение вопроса, которое он предлагает в конце статьи: вывод, полученный им, мог получиться лишь благодаря совершенно произвольному и противоречащему действительности предположению, что знаменатель бесконечной нисходящей прогрессии остается постоянно один и тот же. Кроме того, нельзя соединять знаком равенства несоизмеримые величины.
где
XA — цена продукта A;
NA — общая сумма труда, непосредственно или посредственно истраченного в производстве продукта A,
a - количество продукта a, например, хлеба, потребляемого работником в день;
xa — цена продукта а, например, хлеба;
YA — общая сумма прибыли, полученной всеми производителями, непосредственно или посредственно (т.е. производя материалы и орудия) участвовавшими в производстве продукта А.
Взяв соответственную формулу для любого продукта В, С...
;
;…
и приняв во внимание, что задача теории ценности сводится к определению меновой пропорции, в какой обмениваются продукты, будем иметь
;
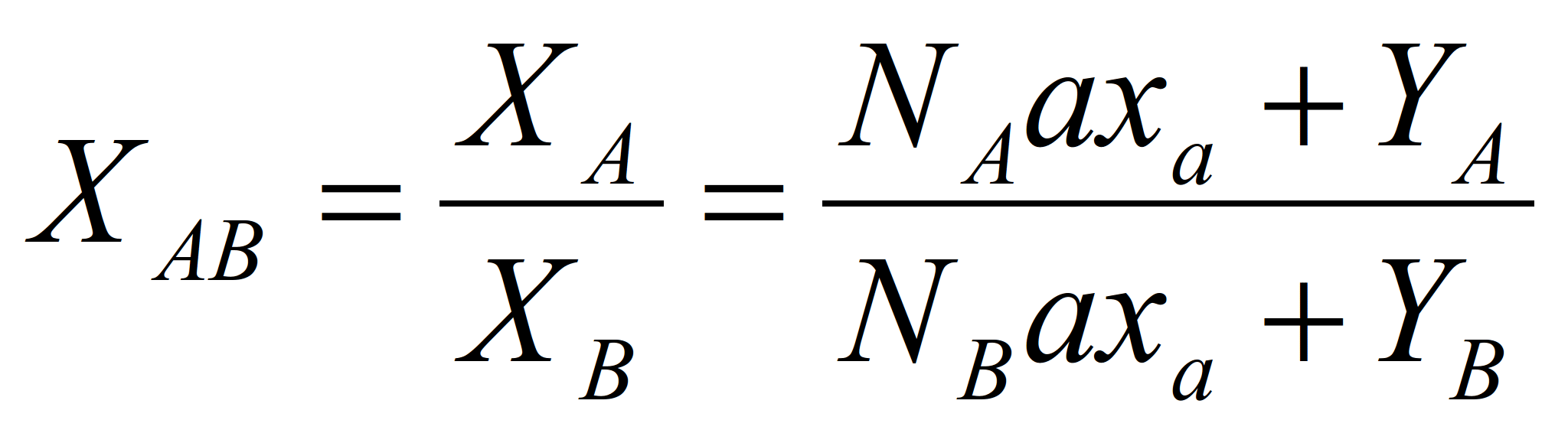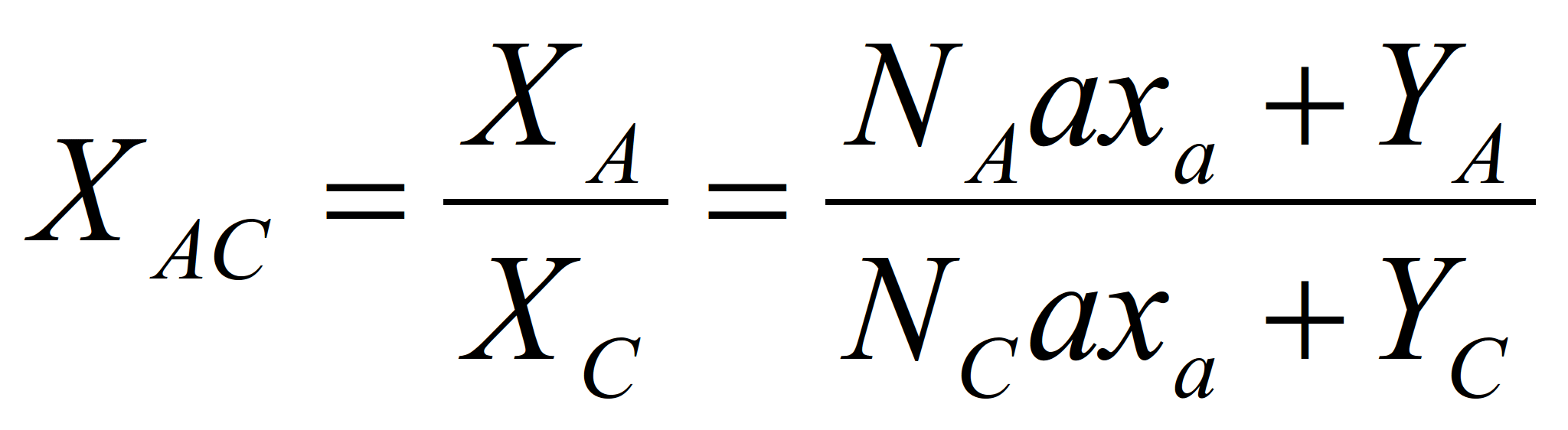и т.д.Далее В.Дмитриев переходит от статических к динамическим моделям: глубина и тщательность работы просто потрясает.
Авторы книги настоятельно рекомендуют аспирантам, докторантам прочесть работы В.Дмитриева, чтобы понять, какими должны быть их научные работы по экономике.
Аргумент «австрийцев», сводящийся к тому, что при определении величины издержек производства нельзя устранить капитал, и, следовательно, в конечном счете, нельзя вычислить общее количество труда, потраченного в производстве продукта, В. Дмитриев парировал с блеском. Он составил систему линейных уравнений (доказав при этом ее принципиальную разрешимость), при помощи которой выразил одновременно произведенные полные затраты труда и тем самым впервые в мировой экономической литературе дал способ выражения, и что особенно важно: метод исчисления, полных затрат труда на единицу продукции с учетом межотраслевых связей, сыгравший важную роль в экономической теории и практике XX в. (см., например: Шухов Н.С. Ценность и стоимость. (Опыт системного анализа). M., 1994. С. 160). Другая точка зрения по этому вопросу содержится в фундаментальном труде известного отечественного историка И.Г. Блюмина, который не дает подобной интерпретации творчества Дмитриева (Блюмин И.Г. Критика буржуазной политической экономии. T. 1. Субъективная школа в буржуазной политической экономии. M., 1962).
Это была по сути первая статическая и динамическая модель межотраслевого баланса (МОБ) в виде линейной системы «затраты-выпуск» с определенными технологическими коэффициентами, сведенными к затратам труда как первичному фактору.
Значение подхода Дмитриева можно оценить, если записать предложенную им систему уравнений в современных обозначениях (см.: Нуги Д.М. Введение к английскому изданию «Экономических очерков». С. 508-510).
Если tj и Tj - прямые и полные затраты труда на производство продукта j, а aij - количество продукта i, необходимое для производства единицы продукта j, тогда система уравнений (1) В.Дмитриева:
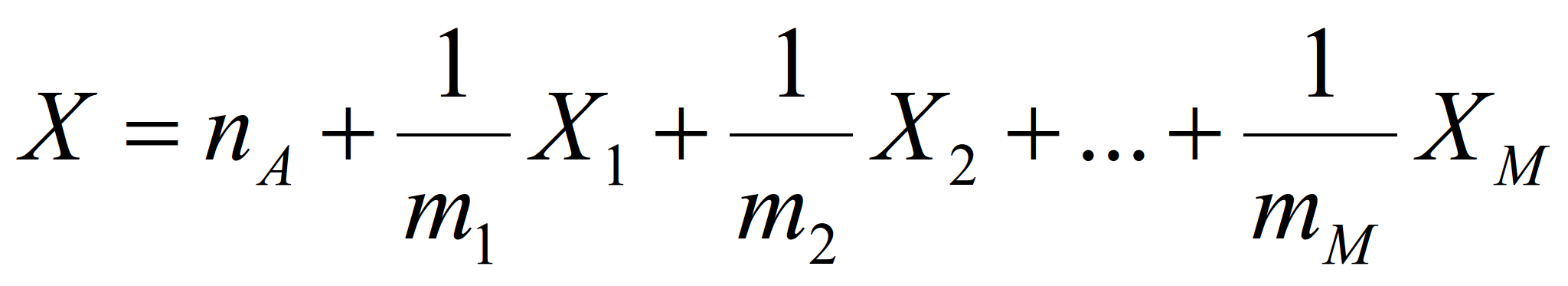
Будет выглядеть так:
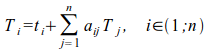
В такой постановке у В.Леонтьева в экономической системе производятся и затрачиваются n продуктов, в то время как В.Дмитриев рассматривает продукты и технические капиталы.
Но если рассматривать производство технических капиталов как самостоятельных продуктов, то модель В.Дмитриева будет эквивалентной современной модели в рамках метода «затраты-выпуск»: коэффициенты X соответствуют величинам T, а 1/mi, — технологическим коэффициентам aij.
Либеральная школа экономистов робко «критикует» работы В.Дмитриева и считает, что идея технологических коэффициентов выдвигалась еще Л.Вальрасом при построении модели общего равновесия.
В своих экономических очерках В.Дмитриев тщательно прорабатывал литературные источники. В работе В.Дмитриев подверг критике либеральную математическую школу и между прочим Л.Вальраса, которые пытались «одни неизвестные определить другими неизвестными». Л.Вальрас подобно своим либеральным коллегам в моделях общего равновесия также безуспешно пытался «одни неизвестные определить другими неизвестными».
Безусловно, интересны исследования немецкого социалиста В.Мюльфорта, который пытался решить проблему трансформации стоимостей в цены производства. В своих работах он построил систему линейных уравнений, в которых издержки производства каждого продукта представлялись как суммы величин, равных ценам единицы затрачиваемого при производстве продуктов, умноженным на технологические коэффициенты. Но, в отличие от В.Дмитриева, использовавшего другой подход, ему не удалось доказать разрешимость полученной системы, в которой содержалось n уравнений и (n + 1) неизвестных.
По мнению ряда авторов: «…С формальной стороны, подход общепризнанного автора законченной теории межотраслевого баланса В.Леонтьева отличался от подхода В.Дмитриева только следующим.
А именно, иным способом решения системы уравнений (вычислялась матрица (E-А)-1, где E — единичная матрица, а А — матрица технологических коэффициентов) и тем, что системы уравнений записывались для всех затрачиваемых факторов, а не только для труда…»
Удивительны утверждения авторов либеральной школы, что «…системы уравнений записывались для всех затрачиваемых факторов, а не только для труда…».
Цитируем В.Дмитриева: «Так как, несмотря на разнообразие и сложность современной техники, даже число всех возможных качественно различных технических капиталов есть все же величина конечная».
Итерационный процесс расчета полных затрат предложенный В.Дмитриевым экономически более корректен, чем модель расчета обратной матрицы В.Леонтьева. Кроме этого этот расчет можно сделать буквально с помощью бухгалтерских счет даже без применения компьютерной техники.
Рассмотрим итерационный процесс расчета полных затрат в 15-ть шагов:
На первом этапе вычисляется сумма двух матриц: матрицы прямых затрат - А и единичной матрицы — Е, т.е. получаем матрицу Е+А.
Далее умножаем вектор удельных прямых затрат труда – L (доля численности занятых в объеме продаж каждой отрасли) или затраты живого труда на матрицу Е+А, получим новые значения, которые обозначим R1
На втором этапе вычисляется сумма двух матриц: матрицы — Е+А, и матрицы - А2 и, т.е. получаем матрицу Е+А+А2.
Далее умножаем вектор удельных прямых затрат труда – L (доля численности занятых в объеме продаж каждой отрасли) или затраты живого труда на матрицу Е+А+А2, получим новые значения, которые обозначим R2:
Потом вычисляем матрицу А3:
На третьем этапе вычисляется сумма двух матриц: матрицы — Е+А+А2, и матрицы — А3 и, т.е. получаем матрицу Е+А+А2+А3.
Далее умножаем вектор удельных прямых затрат труда – L (доля численности занятых в объеме продаж каждой отрасли) или затраты живого труда на матрицу Е+А+А2+А3, получим новые значения, которые обозначим R3:
И цикл повторяется
Как видно из приведенной выше таблицы на каждом этапе итерации вычисления в матрицах (см. выделенные ячейки) точность расчетов увеличивается - А2 (0,057), А3 (0,02), А4 (0,009), А5 (0,005), А6 (0,0026), А7 (0,0014), А8 (8Е-04), А9 (4Е-04), А10 (2Е-04),..., А15 (1Е-05), А16 (7Е-06).
В результате вектор-столбец полных трудовых затрат Ri на каждом этапе итерации рассчитывается более точно, несмотря на простоту расчетов. Это наглядно показано на следующей таблице:
В линейной алгебре известно разложение в степенной ряд матриц:
(E-A)-1=1/(E-A)=E+A+A2+…+Am+…
или
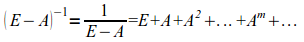
При условии, если Am→0 при m→∞.
при условии Am→0 при
m→∞. Это условие предполагает
разложение в условиях бесконечности
технологических циклов.Цитируем В.Дмитриева: «Так как, несмотря на разнообразие и сложность современной техники, даже число всех возможных качественно различных технических капиталов есть все же величина конечная».
Это можно ему еще как-то простить.
В книге авторы доказывают, что если общество не будет контролировать цены и оплату труда, то кризисы будут происходить регулярно и бесконечно в будущем. Никакие вторичные факторы не могут описывать реальную экономику. Отбросив базовую категорию труда, современные либеральные экономисты попадают очередной раз в замкнутый круг:
Столь же смешно выглядит утверждение, что В.Леонтьев разработал системы уравнений для всех затрачиваемых факторов, а не только для труда. Да, он разработал, только главное потерял – труд. Этим самым он уничтожил базовую идею МОБ В.Дмитриева:
Общий вывод либеральных экономистов состоит, в том, что: «…матричные уравнения для вычисления полных затрат труда у В.Дмитриева и В.Леонтьева совпадают с точностью до тождественных элементарных преобразований, а качественное различие их методов заключается только в том, что
первый позволяет определить затраты данного продукта на производство всех других продуктов;
второй — затраты всех продуктов на производство данного продукта…»
В критике В.Дмитриева либеральные «теоретики» так и норовят найти изъяны в его базовой трудовой модели МОБ. Вот один из любимых аргументов:
«…недостатком такой системы в целом, которую первым построил В.Дмитриев, является ее статический характер, неспособность отражать экономические реалии в динамике…».
Это не удивительно – большинство из современных либеральных «теоретиков» и критиков отличаются слабыми знаниями в области математики хотя бы на уровне гимназического курса математики 19-го века. Естественно, что они так и не смогли добраться через частоколы статических математических моделей МОБ до 61 стр. работы В.Дмитриева. Именно с 61 стр. В.Дмитриев начинает строить плотноупакованные, многоярусные ряды динамических моделей МОБ и уже на 71 стр. он рассматривает многопериодную динамическую модель, цитируем:
«…Тогда, как было показано нами в соответственном месте (при изложении учения Смита), общая сумма издержек производства единицы продукта А (в Рикардовском смысле, т.е. включая сюда и прибыль - r) выразится так:
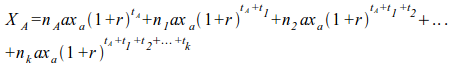
Где
nA, n1, n2,... и т.д. — количества текущего труда, затраченные на производство продукта А;
k1, k2, k3,... технических капиталов участвовавших в производстве продукта A;
tA, t1, t2,... и т.д., означают «период производства» продукта А и технических капиталов k1, k2, k3,....
Далее В.Дмитриев, начиная с 76 стр. и до 106 стр., исследуя динамическую трудовую модель МОБ, естественно вынужден был применять дифференциальные счисления. Так какую «…неспособность отражать экономические реалии в динамике…» имели в виду либеральные горе «теоретики»?
Ответ для авторов книги очевиден: существует минимум пять неспособностей у либеральных экономистов:
Правда, потом после очень напряженного «критического анализа» они «снисходят» до В.Дмитриева и, надувая щеки, заявляют: «…Тем не менее, сегодня считается общепризнанным, что с именем В.Дмитриева связано зарождение экономико-математического моделирования в нашей стране…»
Значение полученного В.Дмитриевым результата было осознано несколько лет спустя. Его исследования были продолжены в СССР в 20-е годы, когда на их основе был построен первый шахматный межотраслевой баланс — пионерный в мировой практике народнохозяйственного планирования. Об этом балансе 1923/1924 гг. в журнале «Плановое хозяйство» (1926. №12) писал и В.Леонтьев, впоследствии удостоенный Нобелевской премии за расчеты межотраслевых балансов США. Знакомый с работами В. Дмитриева, он заимствовал не только идеи указанного баланса, но и методы его построения с помощью системы линейных уравнений (1) и (V), предложенные В.Дмитриевым еще в 1898 г., и развитые в 1922 г. известным в свое время отечественным экономистом Л.Лубны-Герцыком.
В своем исследовании последний использовал не только предложенную В.К. Дмитриевым систему уравнений для определения полных затрат труда, но и так называемую «систему трудовых эквивалентов» (Лубны-Герцык Л. О переводе капитала в трудовые эквиваленты. M., 1922). Практически Л. Лубны-Герцык в 1922 г. впервые вводит среднеотраслевые нормативы в своей «системе трудовых эквивалентов».
Поставив вопрос о возможности сведения затрат, особенно затрат прошлого труда и капитала, к совокупности «трудовых эквивалентов», Л.Лубны-Герцык предложил ряд итеративных процедур для нахождения полных коэффициентов затрат, идея которых несомненно принадлежит В.Дмитриеву.
Идею вычисления и использования полных затрат труда в экономических расчетах поддерживал один из основоположников советской экономико-математической школы академик B.Немчинов, который также указывал на новаторский характер работ В.Дмитриева в теории ценообразования. Считая, что В.Дмитриев предложил вполне приемлемую в народнохозяйственных расчетах формулу для выражения плановой цены, он подчеркивал важность системы линейных уравнений, предложенной русским ученым для вычисления одновременно произведенных полных затрат труда, и выдвинутой В.Дмитриевым идеи технологических коэффициентов затрат продукции одной отрасли на производство продукции других отраслей.
Кроме того, сам B. Немчинов, получивший общую формулу для расчета полных затрат труда в моделях ценообразования, специально разрабатывавшихся для формального и содержательного обобщения марксистской трудовой теории стоимости, также использовал в своих исследованиях уравнения В. Дмитриева.
Он предлагал использовать итерационный процесс решения следующей системы уравнений:
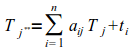
Обратите внимание, B.Немчинов в отличие от В.Леонтьева и австрийской школы использует идею В.Дмитриева о конечности технологических циклов, и поэтому естественно применяет итерационный подход.
Суть этого подхода состоит в том, что сначала задаются величины прямых затрат труда ti и первая итерация полных затрат T*j. Вычисления продолжались бы до тех пор, пока величины T*j не изменялись бы в пределах точности расчетов. Точнее конечности тех или иных технологических цепочек или разделения труда, при производстве того или иного конечного продукта.
Немчинов считал, что «этот итерационный процесс... адекватно отображает не только марксистскую концепцию процесса перенесения стоимости, но также в полной мере соответствует концепции формирования общественно-необходимых затрат труда» и что итерационную формулу предложил В.Дмитриев. Он также полагал, что полные затраты труда были общественно-необходимыми затратами труда на производство продукции по Марксу.
Либеральные экономисты и их «теоретики» требуют внести некоторые «уточнения». Так некоторые из них утверждают следующее:
Во-первых, В.Дмитриев вообще не предлагал никакой итерационной формулы, предполагая решать соответствующую систему уравнений (1) методом последовательного исключения переменных (с. 59, система (V))
Во-вторых, он не был марксистом.
Единственно в чем авторы книги могут согласиться с мнением либеральных экономистов, что В.Дмитриев не был ни марксистом, ни либералом.
Работы В.Дмитриева свидетельствуют о том, что он занимался поиском объективных экономических законов. Корректно их доказывал с использованием доступного математического инструментария того времени, а не придумывал заказанные экономические «законы» теми или иными политическими партиями, тем или иным политическим строем, притягивая за уши математику к их доказательству, в чем поднаторели «теоретики» либерального толка.
В то же время утверждение либеральных «экономистов», что «…Дмитриев вообще не предлагал никакой итерационной формулы, предполагая решать соответствующую систему уравнений (1) методом последовательного исключения переменных (с. 59, система (V))…» лишний раз свидетельствует, что либеральные «экономисты» всегда были далеки от реальной экономики и живут в ими придуманной виртуально-иллюзорной «экономике». Мало того, они элементарно не знакомы с методами решений системы линейных уравнений и не делали никаких расчетов. Авторам книги хотелось бы посмотреть на борзописцев либерального толка: как они будут решать систему уравнений (1) методом последовательного исключения переменных (отраслей по МОБ), когда переменных или отраслей будет не четыре, а допустим около 500 отраслей по стандарту SIC USA или более 1000 отраслей как в современном МОБ США в рамках стандарта NAICS.
Цитируем В.Дмитриева: «… будем иметь систему (V) из четырех уравнений с четырьмя неизвестными …»
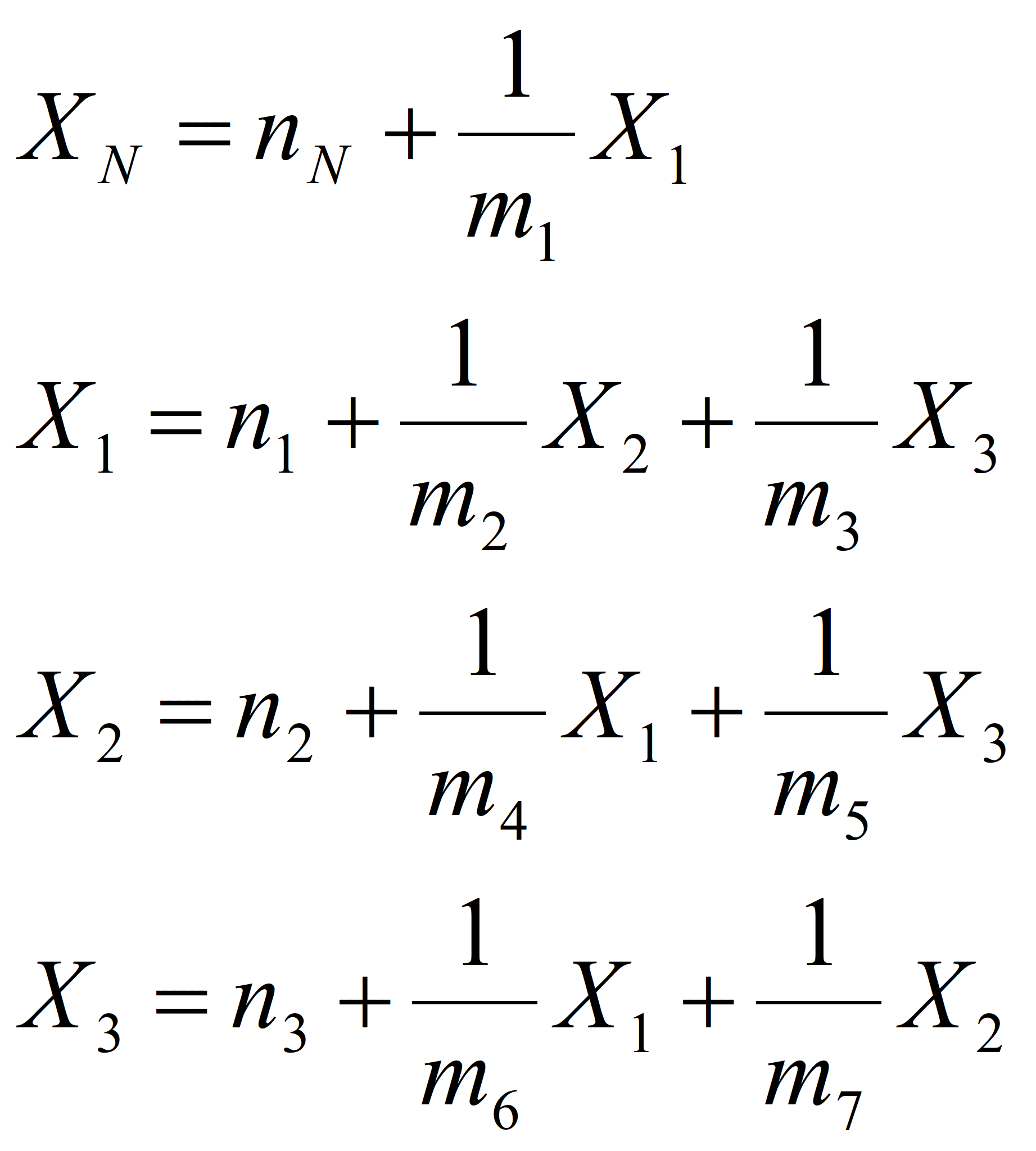(V)
Следует отметить еще одну особенность либеральных «теоретиков». То ли они страдают невнимательностью при прочтении серьезных материалов по исследованию объективных экономических законов. То ли они не знают математики. То ли они сознательно не замечают те или иные важнейшие положения при постановке задачи и далее по исследованию объективных экономических законов. Обратите внимание, Л.Лубны-Герцык, B. Немчинов (в отличие от В.Леонтьева, австрийской школы и либеральных экономистов) использует идею В.Дмитриева о конечности технологических циклов. Поэтому они естественно применяют итерационный подход – он очевиден, когда говорится о конечности технологических циклов.
Цитируем В.Дмитриева: «…Так как, несмотря на разнообразие и сложность современной техники, даже число всех возможных качественно различных технических капиталов есть все же величина конечная…»
Ряд авторов, далеких от реальных ежегодных расчетов МОБ, утверждают, что идея вычисления стоимостей с помощью полных затрат труда потеряла популярность в связи с переходом от статических моделей MОБ к динамическим, содержащим баланс фондов и задающим процесс накопления в явном виде.
В 2006 г. при прогнозе и расчете кризисов 2008-2010 г.г. авторами использовалась не статическая, а именно динамическая модель В.Дмитриева. Авторов книги интересовала динамика увольнений в 2008г. Затем величина безработицы в США в 2009 г., и далее дальнейший ее рост в 2010 г. Данный прогноз и расчеты невозможно сделать без учета вычисленных авторами книги отраслевых мультипликаторов полных затрат, т.е. прямых и косвенно-латентных связей или затрат.
Поэтому авторский прогноз динамики сжатия экономики США, безработицы и ее фазовой динамики отличался от реальных данных статистических ежемесячных отчетов Минтруда США на величину ошибки не более 10-20% с учетом данных месячной трудовой статистики США на март 2010 г.
Но ведь кризис еще не закончился, поэтому ошибка авторов в прогнозах 2006 г. безработицы в США на период 2008-2010 г.г. с каждым месяцем будет уменьшаться.
Отметим, при условии расчета по итерационной методике В.Дмитриева, логично вытекающей из конечности технических капиталов, можно осуществить расчет фазовой динамики, т.е. всех этапов кризиса, а не просто прогноз масштаба сжатия экономики США по каждой отрасли. А также вычислить итоговую величину роста безработицы за период 2008-2010 г.г., как это предлагает методика В.Леонтьева.